I created this on my phone in MATLAB. You can probably do this in Octave with similar or the same code.

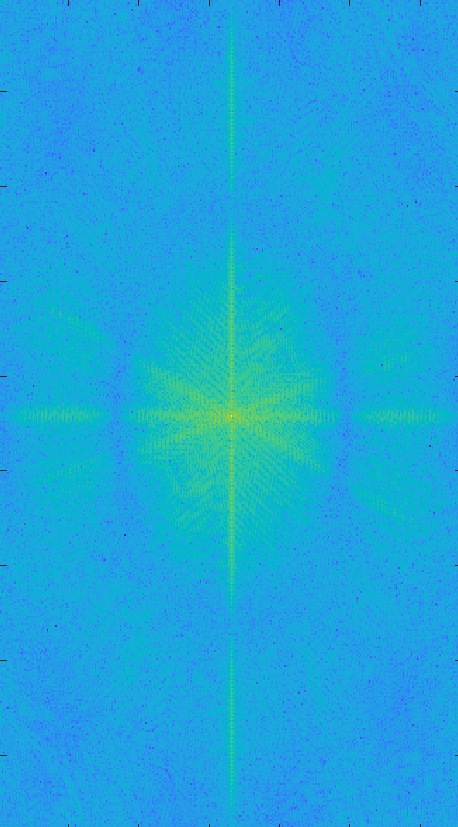
First, I downloaded the image from Lemmy, then uploaded it into my MATLAB app. I renamed the image to image.jpg, then ran the following code:

image=imread(“image.jpg”) imagesc(log10(abs( fftshift(fft2(image)) )))

fft2 applies a 2D Fast Fourier transform to the image, which creates a complex (as in complex numbers) image. abs takes the magnitude of the complex image elementwise. log10 scales the result for display.

Then I downloaded the image from the MATLAB app, went into the Photos app and (badly) cropped out the white border.

Despite how dramatically different it looks, it actually contains the same [1] information as the original image. Said differently, you can actually go back to the original with the inverse functions, specifically by undoing the logarithm and applying the inverse FFT.

[1] Almost. (1). There will be border problems potentially caused by me sloppily cropping some pixels out of the image. (2). It looks like MATLAB resized the image when rendering the figure. However, if I actually saved the matrix (raw image) rather than the figure, then it would be the correct size. (3) (Thank you to @itslilith@lemmy.blahaj.zone for pointing this out.) You need the phase information to reconstruct the original signal, which I (intentionally) threw out (to get a real image) when I took the absolute value but then completely forgot about it.